Thermistor Non-Linearity
We learned how to use a thermistor in a voltage divider and how to calculate the thermistor resistance at a given moment. The next step is to determine the temperature corresponding to that resistance.
This step is not simple. Thermistors are non-linear devices, which means resistance does not change in a straight line with temperature. Because of this, resistance cannot be converted to temperature using a single linear formula.
The non-linear curve problem
A thermistor does not change resistance evenly as temperature changes. The relationship between temperature and resistance follows a curve.
At lower temperatures, a small change in temperature produces a large change in resistance. At higher temperatures, the same temperature change produces a much smaller resistance change. This behavior is a fundamental property of thermistors.
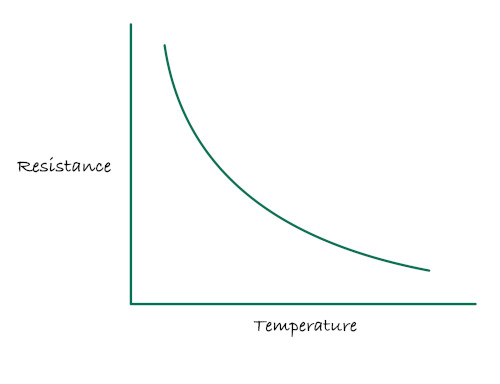
Because of this curve, there is no simple rule such as:
a fixed number of ohms equals one degree
Using known reference points
Thermistor manufacturers are aware of this behavior and provide detailed datasheets. These datasheets list resistance values at specific temperatures.
Each entry in the datasheet represents a known and measured point on the thermistor curve. Together, these points describe how resistance changes across the temperature range.
Common approaches used in practice
There are three widely used methods to convert thermistor resistance into temperature:
Beta equation (B parameter method):
This method uses a single material constant called the Beta value. The value is provided in the thermistor datasheet. This method assumes the curve can be approximated using a logarithmic relationship between resistance and temperature.
The Steinhart-Hart equation:
The Steinhart-Hart equation is a more accurate model of the thermistor curve. Instead of a single constant, it uses three coefficients that better fit the non-linear behavior.
These coefficients are either provided by the manufacturer or derived from calibration data. Steinhart-Hart offers high accuracy across a wide temperature range. The cost is increased computation and more complex implementation.
Lookup tables:
A lookup table stores known temperature and resistance pairs. These values are taken directly from the thermistor datasheet or from calibration measurements. When a resistance is measured, it is compared against the table to find the closest matching temperature. If the resistance lies between two entries, interpolation can be used to estimate the temperature between them.
In the next chapters, we will see in detail how to use B equation and Steinhart-Hart equation to determine the temperature.